10332. Посадка травы

Наступило время для фермера Джона сажать траву на всех своих полях. Вся ферма состоит из n полей, пронумерованных 1 ... n и соединенных n – 1 двунаправленными дорогами таким образом, что с каждого поля можно достичь любое другое поле используя некоторый набор путей.

Фермер Джон может сажать разные типы травы на каждом поле, однако он хочет свести к минимуму количество используемых видов травы в целом, поскольку чем больше видов травы он использует, тем больше затрат он несет.

К сожалению, его коровы стали относиться к выбору травы на ферме довольно снобистски. Если один и тот же тип травы посажен на двух соседних полях (напрямую соединенных дорогой) или даже на двух почти соседних полях (которые напрямую связаны с общим полем дорогами), то коровы будут жаловаться на отсутствие разнообразия в их питательном рационе. Последнее что нужно фермеру Джону, так это жалобы от коров, учитывая, сколько вреда они, как известно, причиняют, будучи недовольны.

Помогите фермеру Джону определить минимальное количество видов травы, которое ему нужно для всей фермы.

Вход. Первая строка содержит число n (1 ≤ n ≤ 10⁵). Каждая из оставшихся n – 1 строк описывает дорогу и содержит два поля, которые она соединяет.

Выход. Выведите минимальное количество видов травы, которое нужно использовать фермеру Джону.

Пример входа	Пример выхода
4 1 2 4 3 2 3	3

РЕШЕНИЕ

графы

Анализ алгоритма

Вершины дерева следует раскрасить наименьшим количеством красок так, чтобы один цвет не имели:

· две вершины, соединенные ребром;

· две вершины на расстоянии двух ребер;

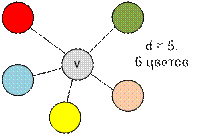
Пусть некоторая вершина v имеет степень d. Это значит, что из вершины v исходит d ребер. Тогда нам необходимо как минимум d + 1 цвет для покраски вершины v и всех ее смежных вершин.

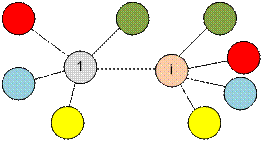
Пусть максимальная степень вершины в графе равна d. Покажем, что существует требуемая раскраска из d + 1 цветов. Возьмем вершину 1, покрасим ее цветом 1. Пусть она имеет d соседей, покрасим их в цвета 2, 3, …, d + 1. Возьмем вершину i – соседа 1, покрашенную в цвет i. Пусть она также имеет d соседей. Вершина i имеет цвет i, один из ее соседей покрашен в цвет 1. Остальных соседей вершины i можно красить цветами 2, 3, …, i – 1, i + 1, …, d + 1. Поскольку структура – дерево, то таким образом можно покрасить все вершины.

Пример

Граф из примера можно раскрасить тремя цветами:

Реализация алгоритма

Объявим массив для подсчета степеней вершин графа. Степень вершины i будем хранить в d[i].

int d[100000];

Читаем входные данные. Подсчитываем степени вершин графа.

scanf("%d", &n);

for (i = 0; i < n - 1; i++)

{

scanf("%d %d", &a, &b);

d[a]++; d[b]++;

}

В переменной res находим максимальную степень вершины.

res = 0;

for (i = 1; i <= n; i++)

if (d[i] > res) res = d[i];

Выводим ответ.

printf("%d\n", res + 1);